During this week, I implemented all the remaining functions of Phase-3. These included plot_shear_stress(), max_shear_force(), max_bending_moment(), and max_deflection() functions. As this was the last week of GSoC, I also had to prepare a report stating all the work I did during summer. The report can be found here.

`plot_shear_stress()`

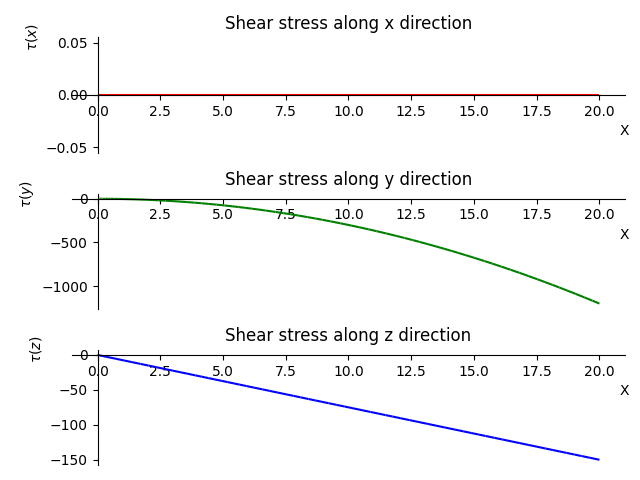
This function plots the shear stress along a specifed direction. If no direction is specified, all plots are displayed. Here is an example:

    >>> from sympy.physics.continuum_mechanics.beam import Beam3D
    >>> from sympy import symbols
    >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x')
    >>> b = Beam3D(20, E, G, I, 2, x)
    >>> b.apply_load(15, start=0, order=0, dir="z")
    >>> b.apply_load(12*x, start=0, order=0, dir="y")
    >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])]
    >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4')
    >>> b.apply_load(R1, start=0, order=-1, dir="z")
    >>> b.apply_load(R2, start=20, order=-1, dir="z")
    >>> b.apply_load(R3, start=0, order=-1, dir="y")
    >>> b.apply_load(R4, start=20, order=-1, dir="y")
    >>> b.solve_for_reaction_loads(R1, R2, R3, R4)
    >>> b.plot_shear_stress()

`max_shear_force()`

This function calculates the value of max shear force along all directions and returns a list of tuples containing the point of max shear and its shear value.

    >>> from sympy.physics.continuum_mechanics.beam import Beam3D
    >>> from sympy import symbols
    >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x')
    >>> b = Beam3D(20, 40, 21, 100, 25, x)
    >>> b.apply_load(15, start=0, order=0, dir="z")
    >>> b.apply_load(12*x, start=0, order=0, dir="y")
    >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])]
    >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4')
    >>> b.apply_load(R1, start=0, order=-1, dir="z")
    >>> b.apply_load(R2, start=20, order=-1, dir="z")
    >>> b.apply_load(R3, start=0, order=-1, dir="y")
    >>> b.apply_load(R4, start=20, order=-1, dir="y")
    >>> b.solve_for_reaction_loads(R1, R2, R3, R4)
    >>> b.max_shear_force()
    [(0, 0), (20, 2400), (20, 300)]

`max_bending_moment()`

This function calculates the value of max bending moment along all directions and returns a list of tuples containing the point of max bending moment and its bending moment value.

    >>> from sympy.physics.continuum_mechanics.beam import Beam3D
    >>> from sympy import symbols
    >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x')
    >>> b = Beam3D(20, 40, 21, 100, 25, x)
    >>> b.apply_load(15, start=0, order=0, dir="z")
    >>> b.apply_load(12*x, start=0, order=0, dir="y")
    >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])]
    >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4')
    >>> b.apply_load(R1, start=0, order=-1, dir="z")
    >>> b.apply_load(R2, start=20, order=-1, dir="z")
    >>> b.apply_load(R3, start=0, order=-1, dir="y")
    >>> b.apply_load(R4, start=20, order=-1, dir="y")
    >>> b.solve_for_reaction_loads(R1, R2, R3, R4)
    >>> b.max_bending_moment()
    [(0, 0), (20, 3000), (20, 16000)]

`max_deflection()`

This function calculates the value of max deflection along all directions and returns a list of tuples containing the point of max deflection and its deflection value.

    >>> from sympy.physics.continuum_mechanics.beam import Beam3D
    >>> from sympy import symbols
    >>> l, E, G, I, A, x = symbols('l, E, G, I, A, x')
    >>> b = Beam3D(20, 40, 21, 100, 25, x)
    >>> b.apply_load(15, start=0, order=0, dir="z")
    >>> b.apply_load(12*x, start=0, order=0, dir="y")
    >>> b.bc_deflection = [(0, [0, 0, 0]), (20, [0, 0, 0])]
    >>> R1, R2, R3, R4 = symbols('R1, R2, R3, R4')
    >>> b.apply_load(R1, start=0, order=-1, dir="z")
    >>> b.apply_load(R2, start=20, order=-1, dir="z")
    >>> b.apply_load(R3, start=0, order=-1, dir="y")
    >>> b.apply_load(R4, start=20, order=-1, dir="y")
    >>> b.solve_for_reaction_loads(R1, R2, R3, R4)
    >>> b.solve_slope_deflection()
    >>> b.max_deflection()
    [(0, 0), (10, 495/14), (-10 + 10*sqrt(10793)/43, (10 - 10*sqrt(10793)/43)**3/160 - 20/7 + (10 - 10*sqrt(10793)/43)**4/6400 + 20*sqrt(10793)/301 + 27*(10 - 10*sqrt(10793)/43)**2/560)]

This blog marks the end of my GSoC project. I have successfully completed everything I stated in my project and all the work has been merged as well. This summer was a great learning experience for me. I would like to thank Google for organizing this program, Sympy for being an amazing organisation and my mentors Ishan Joshi and Nikhil Maan for always supporting me and guiding me throught this project.