During this week, I implemented the solve_for_ild_shear() function. This function uses the solve_for_ild_reactions() function and calculates the I.L.D. equations for shear at a point specified by the user. The derived equations can then be plotted using the plot_ild_shear() function.

solve_for_ild_shear()

This function calculates the shear equations in terms of ‘x’. Here ‘x’ represents the distance of the moving load from the origin. Here is an example:

    >>> from sympy import symbols
    >>> from sympy.physics.continuum_mechanics.beam import Beam
    >>> E, I = symbols('E, I')
    >>> R_0, R_8 = symbols('R_0, R_8')
    >>> b = Beam(12, E, I)
    >>> b.apply_support(0, 'roller')
    >>> b.apply_support(8, 'roller')
    >>> b.solve_for_ild_reactions(1, R_0, R_8)
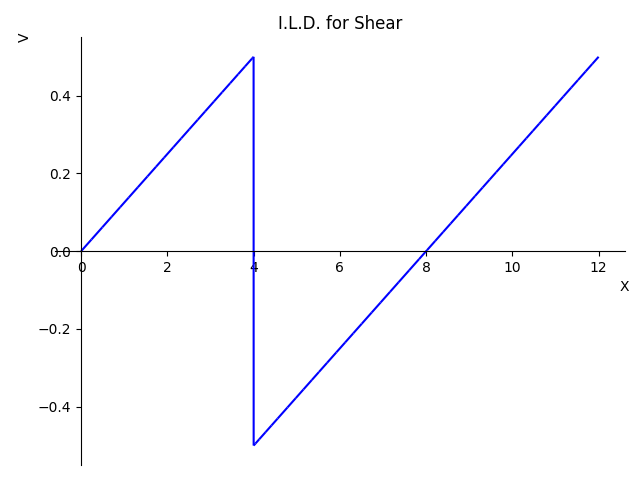
    >>> b.solve_for_ild_shear(4, 1, R_0, R_8)
    >>> b.ild_shear
    Piecewise((x/8, x < 4), (x/8 - 1, x > 4))

plot_ild_shear()

This function plots the above solved equations

    >>> b.plot_ild_shear()

After this gets merged, I will push the last function of phase 2 as well.